大致写一些关于左倾红黑树的总结

附 Visualizing 红黑树:

2-4 tree: http://cs.armstrong.edu/liang/animation/web/24Tree.html

Left-Leaning-Red-Black: http://inst.eecs.berkeley.edu/~cs61b/fa17/materials/demos/ll-red-black-demo.html

红黑树是啥

左倾红黑树可以看作2-3树的一种实现

2-3 树
1. 1. 2-3 树是一种平衡二叉树，而既然红黑树是2-3树的一种实现。可以将红黑树的具体操作进行抽象，对应2-3树的相关操作。
  2. 而具体到红黑树，为了让红黑树实现出2-3树的操作，就需要使用红黑树的思维来考虑2-3树的实现，但同时，要理解红黑树的繁琐操作，就要一直想到，这一系列过程是对应这2-3树的一个操作的。
2. 2-3树的插入与删除
  
  一个结点可以是2结点和3结点，分别含有1或2
  个元素
  点击下列规则对应链接，可查看红黑树对应的实现

  1. 插入:

     1. 规则 [1.1](#1.1):

        > 插入时， 如果父结点为2结点， 合并为3结点， 不产生新结点。

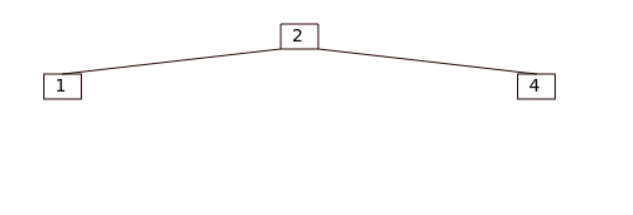        ![source](https://i.loli.net/2018/04/15/5ad3566b29b25.png) => ![des](https://i.loli.net/2018/04/15/5ad3566b3ab95.png)

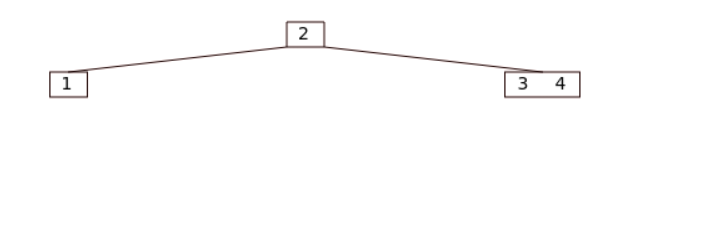
     2. 规则 [1.2](#1.2):

        > 如果父亲为3结点， 合并为4结点， 并且将4结点分裂成一个父2结点和两个子2结点

        ![source]() => ![des]()

  2. 删除:

     删除过程允许临时4结点存在， 在删除结束后从底向上配平4结点

        <span id="2.1_back"></span>

     1. 规则 [2.1](2.1):

        > 对于删除最底部结点， 需要使被删除元素所在结点为3结点

        删除10

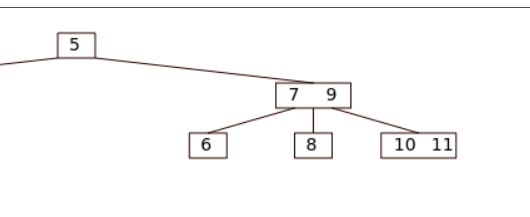
        ![source](https://i.loli.net/2018/04/15/5ad356c77aa89.png)

        以下规则将被删除结点转为3结点

        <span id="2.2_back"></span>

     2. 规则 [2.2](#2.2):

        > 为保证能将目标结点转换为3结点， 需要在自顶向下的搜索过程中将经过路径的结点转换为3结点

     

        经过路径: 如所要元比该结点的元小， 那么左树将是他的经过路径

        <span id="2.3_back"></span>

     3. 规则 2.3:

        > 当经过路径上的下一结点已是3结点时， 不用执行转换

        当目前结点为5时， 检查到左子结点为3结点， 不进行转换

       ![source](https://i.loli.net/2018/04/15/5ad356c77aa89.png) =>

        下面将以删除最小元为例， 括号表示对最小元是这样， 但对其他元来说可能有变化

        <span id="2.4_back"></span>

     4. 规则 2.4:

        > 如果(左)结点为2结点， 而兄弟结点为3结点， 那么将从它的兄弟结点中获取一个元。



        表现为元的重组， 将兄弟结点的最小元作为新的父结点， 将父结点添加到目标路径结点中， 此时兄弟结点转变成2结点(少了一个元)

        <span id="2.5_back"></span>

     5. 规则 [2.5](#2.5):

        > 如果左结点与右结点都为2结点， 那么父亲结点将一个结点给目标结点

        1. 规则 2.5.1:

           > 如果父结点为2结点， 则把父结点与两子结点合成一个新的4结点。

           

        2. 规则 2.5.2:

           > 如果父结点为3或4结点， 则将父结点的最(小)元与两子结点合成一个新的4结点。

           

        合成一个4结点是为了让路径上的结点能够方便获取与送出元素

        以上， 3结点转换结束。

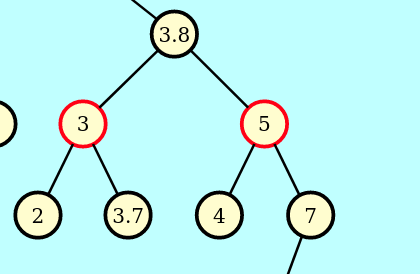
左倾红黑树
1. 特征:
  1. 红黑树只有2结点，但通过颜色来虚拟出n结点
  2. 某结点为红色，表示其与父结点 为一个虚拟结点
  3. 对于左倾红黑树最终过程，只能是左子结点为红色
  4. 一个结点的父子结点不能同为红色
    
    对与3结点来说，颜色为红色的必然是该结点最小元，旋转的实质也就是排序
2. 具体实现
  
  此红黑树是 2-3 的一种具体实现
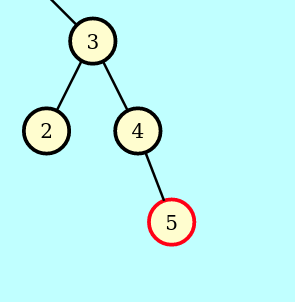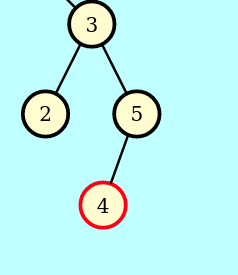
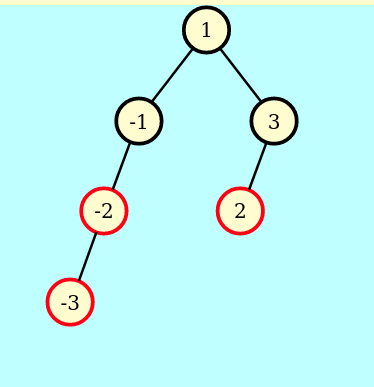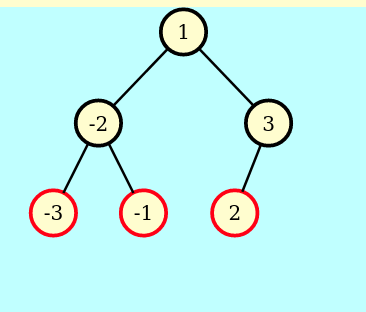
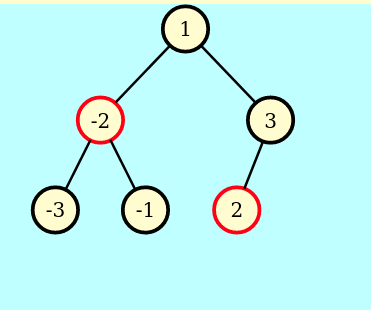
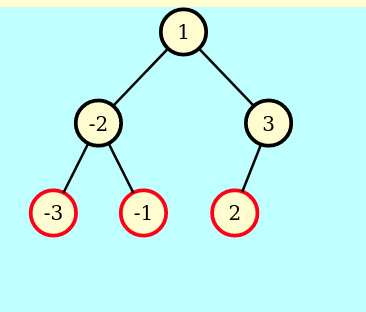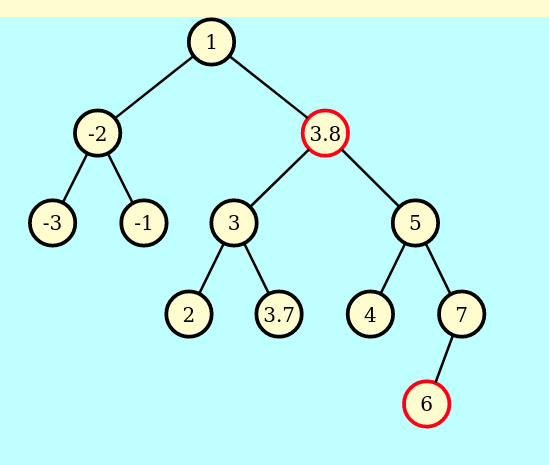
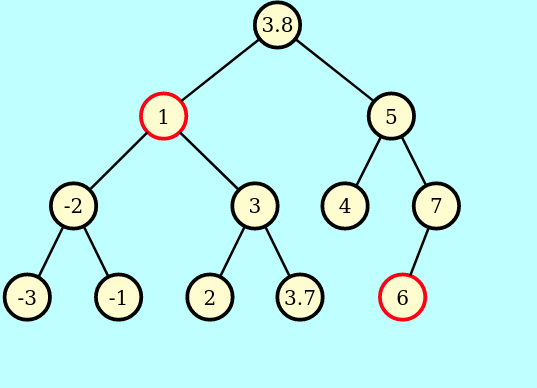  1. 类在的方法:
    1. 旋转
      
      只让左子实际结点为红色 => 只让3虚拟结点^[1]的最小元素为红色=> 虚拟结点元素排序
      
      不会改变结点元素个数与组成
      
      特征:
      - 没有改变元素的映射顺序^[2]
      - 只是单纯改变颜色以及父子关系
      1. 左旋转
        
        把右结点红色转换为左结点红色
        
        将原右结点变为父亲，原父结点变为左儿子
        
        大局上看，以两个结点为单位
        
        =>
      2. 右旋转
        
        目的: 处理连续左结点红色的情况，对应特征4
        
        将原父结点变为右儿子，将原左子结点变为父亲
        
        =>
  2. 2-3树的具体实现
    1. 颜色翻转( colorFlip )
      1. 对应规则 1.2
      将两子实际结点颜色变为黑色，将父实际结点变为红色=> 分解4结点，变成一个2/3父虚拟结点(如果是根结点(实际)变为2结点，如果不是，变为3结点)连接两个2实际(虚拟)结点
      
      =>
    2. 把红色移动给左(右)实际结点(moveRedLeft)(moveRedRight)
      1. 对应规则 2.4
      将兄弟虚拟结点的一个结点给路径虚拟结点，具体实现涉及到父实际结点与子实际结点的变换
      
      =>
    3. 耦合成4结点
      1. 对应规则 2.5
        
        将父实际结点颜色设为黑色，将两子实际结点设置为红色 => 将父虚拟结点的最小元素^[3]传递给子虚拟结点形成一个新的虚拟4-结点
      =>